¿Cuánto plástico es mucho plástico?
A lo largo de los últimos años se han publicado una gran cantidad de estudios informando sobre la presencia de microplásticos en los más diversos ambientes. El plástico ha llegado lugares lejanos como la Antártida y está también en nuestros alimentos, exponiéndonos directamente a sus posibles efectos tóxicos. Cuando estos estudios llegan a la opinión pública se suele pasar por alto que los plásticos, como material particulado que son, no tienen una única métrica de exposición. Es decir, cuando nos exponemos a una cierta cantidad de un compuesto químico, el hecho de cuantificar la exposición en términos de masa (miligramos por litro o por peso corporal) o en moles (milimoles por litro o por unidad de masa) es indiferente. Sin embargo, no ocurre lo mismo con los microplásticos (y tampoco con los nanoplásticos, aunque estos tienen alguna especificidad que merece un tratamiento aparte).
Los plásticos interactúan con su entorno a través de su superficie, que será tanto mayor cuanto menor sea su tamaño y menos esférica sea su forma. En particular, la capacidad de un plástico para lixiviar los aditivos que contiene depende de su superficie y no hay que olvidar que los aditivos son una fuente importante de exposición a contaminantes antropogénicos para los seres vivos. Si la partícula no se aleja mucho de una forma esférica, su tamaño (medido como el diámetro promedio o como el diámetro de la esfera con el mismo volumen que la partícula) se relaciona directamente con la raíz cuadrada de la superficie. En otras geometrías, como en el caso de las fibras, las relaciones tamaño-superficie y entre estas y la masa de las partículas son también fáciles de deducir. Se puede encontrar información al respecto en este artículo. El problema viene cuanto comparamos concentraciones en número con concentraciones en masa.
En un artículo publicado recientemente en Proceedings of the National Academy of Sciences of the United States of America, los autores utilizaron una técnica llamada escaneo hiperespectral por dispersión Raman estimulada (SRS), que aunque compleja y laboriosa es adecuada para la identificación espectral de partículas de menos de 1 µm. En su artículo, aplican SRS a agua embotellada y encuentran concentraciones en número de unas doscientas mil partículas por litro (2.4 ± 1.3 × 105 , de las cuales la gran mayoría son menores de una micra). Por otro lado, un estudio llevado a cabo por nuestro grupo de investigación y publicado en Scientific Reports sobre muestras de agua embotellada de las principales marcas del mercado español dio un valor medio de 0.73 (0.64–1.58) microplásticos por litro, es decir, unas trescientas mil veces menos. Y desde luego encontrar un plástico en una botella de 1.5 litros parece mucho menos peligroso que encontrar 360000.
La diferencia, obviamente, está en el tamaño. Las estimaciones de concentración en masa llevadas a cabo por el grupo de la Universidad de California fueron de unos 10 ng/L, mientras que nuestros datos indican una concentración en masa para partículas < 100 µm de 176 ng/L. El tamaño mediano de los microplásticos (< 100 µm) de nuestras muestras fue de 75 µm (esfera del mismo volumen que la partícula), mientras que las partículas del grupo de la Universidad de California estaban entre 100-200 nm y 1-2 µm. Con las concentraciones medidas por nuestro grupo, que considerando todas las partículas y no solo las menores de 100 µm alcanzan un valor de 1.61 (1.10-2.88) µg/L, una persona que consuma 2 litros de agua al día tardaría aproximadamente 850 años en ingerir un gramo de plástico; eso sí, dividido en medio millón de pequeños fragmentos.
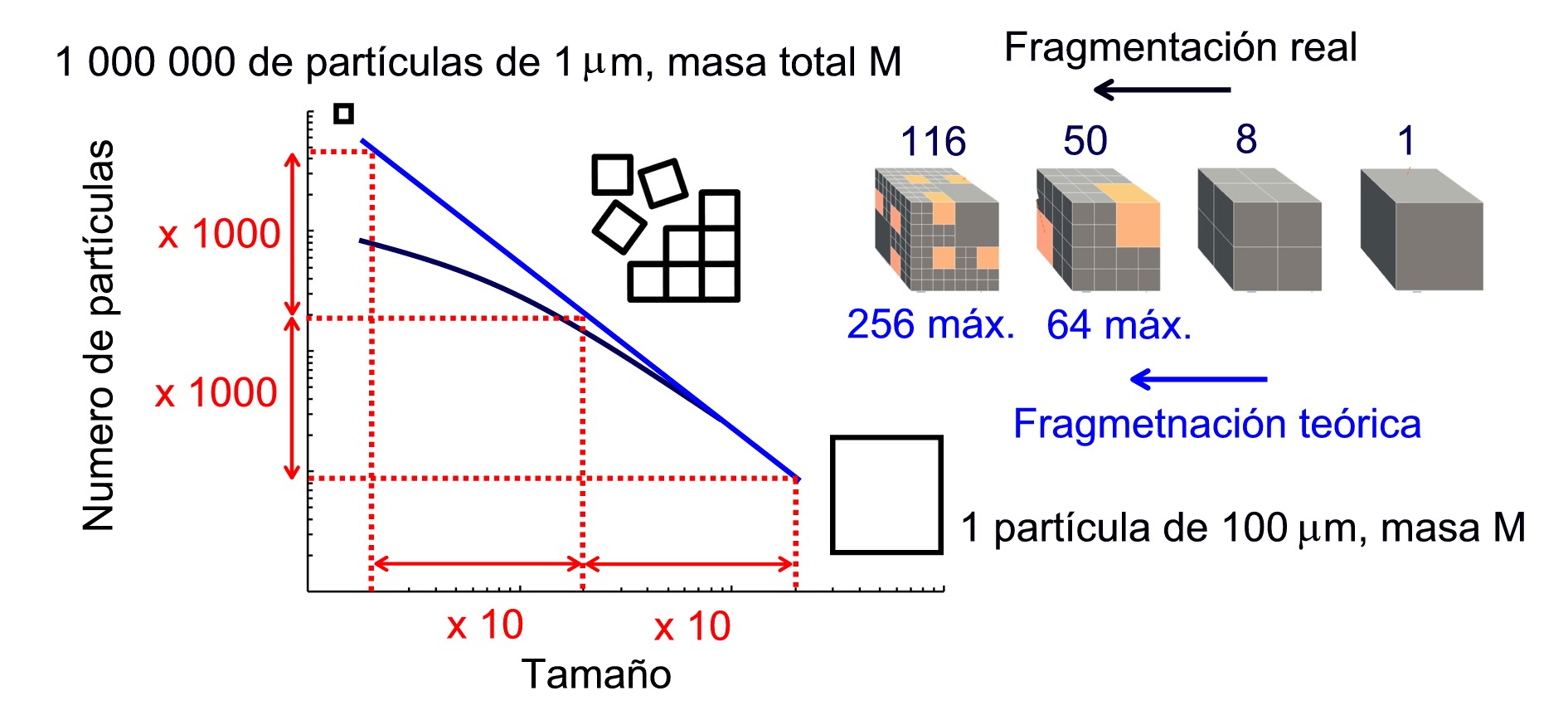
Está ampliamente demostrado que los microplásticos pequeños se producen por la fragmentación de los mayores, salvo en el caso de ciertos materiales fabricados específicamente con ese tamaño y cuya comercialización está regulada con rigor creciente. También es sabido que una fragmentación fractal (es decir, la que mantiene patrones de autosemejanza a diferentes escalas) conserva la masa y si la dimensión de esta se aproxima a la de los objetos que se fragmentan (3, en plásticos tridimensionales), la masa que se distribuye entre 0 y 10 µm es la misma que entre 10 y 20 µm, que su vez será la décima parte de la que habría entre 0 y 100 µm. Dicho de otra forma, un plástico de 75 µm generaría un máximo de 1000 (10 x 10 x 10) de 7.5 µm y 1000000 de 750 nm, pero la masa sería siempre la mismo. Y esta es la clave de la diferencia de trescientas mil partículas de plástico por litro a un plástico por botella. En ambos casos la masa de plástico es bastante parecida y la discrepancia se puede explicar por la menor cantidad de partículas pequeñas que se producen en una fragmentación real como se ilustra en la figura siguiente. De hecho, la desviación de la ley de la potencia para tamaños pequeños es un fenómeno bien conocido y ha sido evidenciado ya hace bastante años en estudios sobre la presencia de microplásticos en el medio ambiente.
Este juego de concentraciones en número y masa se da con frecuencia, hace las delicias de los periodistas y los investigadores lo hemos utilizado con frecuencia (tal vez demasiada) para enfatizar nuestros hallazgos. Por ejemplo, el efluente de una depuradora que estudiamos en un trabajo anterior emite 10.7 microplásticos por litro, que multiplicado por el caudal de agua depurada arroja unos 300 millones de microplásticos al día por tan solo una de las muchas depuradoras (150 tan solo en Madrid) que vierten a la Cuenca del Tajo, donde viven alrededor de 10 millones de personas entre España y Portugal. Parecería que el Tajo a su desembocadura en Lisboa debería de ser una gran corriente de plástico y sin embargo no es así.
La clave, al igual que en el caso anterior está en el tamaño y la masa. Si se utiliza la geometría de las partículas pare obtener una estimación de la concentración en masa, tal como indicamos en un artículo reciente aparecido en la revista Science of the Total Environment, esta resulta ser de 15 µg/L, equivalente a 430 gramos de plástico por día, que, aun constituyendo un contaminante potencialmente peligroso, ya no parece tan impresionante, sobre todo considerando que esa misma depuradora vertía casi treinta mil toneladas de agua depurada al día durante el período estudiado.
Otro ejemplo de cálculo creativo lo tenemos en el depósito atmosférico. En otro trabajo anterior, realizado en colaboración con diversos grupos españoles, medimos las tasas de depósito de plástico mediante un sistema de muestreadores pasivos como los que se describen en esta entrada anterior. Los cálculos arrojaron tasas de depósito de entre 5.6 y 78.6 microplásticos por metro cuadrado y día, con los valores más elevados correspondientes a las áreas más pobladas, especialmente Madrid y Barcelona. Si consideramos una plaza grande, como la Puerta del Sol en Madrid o Trafalgar Square, ambas con unos 12000 metros cuadrados de superficie, las tasas diarias de depósito rondarían el millón de microplásticos por día.
Como en el caso anterior la razón para no ver tanto plástico es el tamaño. A partir de las medidas geométricas de las partículas, hemos estimado una tasa media de depósito en masa de 50.9 gramos por kilómetro cuadrado al día que extrapolado a la superficie de las plazas mencionadas, arroja un depósito aproximado de un gramo diario, equivalente al peso de un envoltorio de caramelo. Claro que este material no se encuentra en una sola pieza, sino dividido en partículas diminutas, principalmente fibras, que constituyen el componente predominante del plástico atmosférico. Si estas pequeñas fibras o fragmentos representan un riesgo para la salud es una cuestión compleja que aún está en investigación y que se abordará en futuras publicaciones.